Output Voltages on RF Wheatstone Bridges

Introduction

Much of the online material about Wheatstone bridges focusses on the case where the bridge is balanced, or nearly balanced ($\vert Z_l\vert$ ~ 50 ohms in this case). In an instrument that uses a bridge with fixed reference resistors to measure unknown impedance values, we need to work out the unknown impedance from measurements on an unbalanced bridge. The diagram below shows a generic case of such a bridge.

When using detectors that respond to amplitude only, there are three independent voltages that can be measured, shown as $V_r$ , $V_z$ and $V_a$ . These three voltages are all dependent on $V_f$ (or $2V_f$, the generator voltage, if that’s easier to visualise). $V_z$ and $V_a$ are independent from each other because, whilst in vector terms $2V_f = V_z + V_a$, the magnitude of these quantities does not follow this rule if $Z_l$ is not a pure resistance.

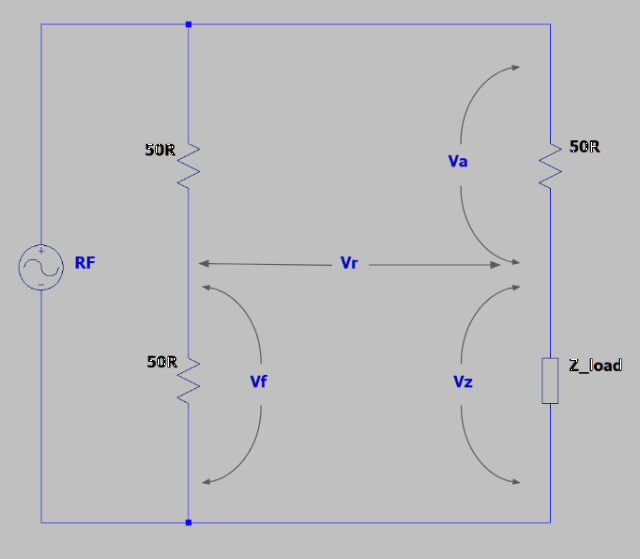
From here onwards, assume that all voltages are scalar quantities (i.e. refer to the magnitude of the complex voltage) unless stated otherwise.

Bridge Voltage Magnitudes

We can calculate the expected magnitude of these voltages as follows.

$V_a$ and $V_z$ are voltages across the two impedances of a simple potential divider, albeit with one of the impedances potentially complex.

If, for example, $2V_f$ is 1.0, the magnitude of the current flowing through the load and upper resistor will be $\frac{1}{\vert Z_l+50\vert }$

Multiplying this by 50 for the upper resistor and and $\vert Z_l\vert $ for the unknown load gives the magnitude of the voltages relative to $2V_f$. Hence,

$$V_a=2V_f\frac{50}{\vert Z_l+50\vert }$$

$$V_z=2V_f\frac{\vert Z_l\vert }{\vert Z_l+50\vert }$$

To get at $V_r$ we simply note that in *vector* terms, $V_r = V_f - V_z$ , and the magnitude $V_r$ is then $\vert V_f - V_z\vert $ .

On the left of the bridge we have $V_f$, and on the right we use potential divider maths again to get the midpoint voltage. Then, with complex-valued calculations inside the $\vert mod\vert $ bars, we have

$$V_r = \vert 2V_f \frac{Z_l}{Z_l+50} - V_f\vert $$